Dati cinque punti nel piano, in modo che a tre a tre non siano allineati, quante rette passanti per due di questi punti è possibile tracciare? Sai esprimere il legame generale tra il numero N di punti ed il numero M di rette che si possono tracciare?
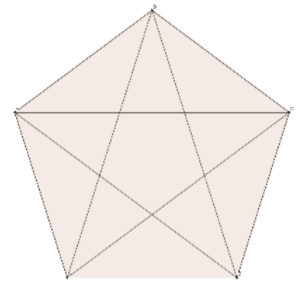
Nel rappresentare sul piano cinque punti a tre a tre non allineati e le rette passanti ci si accorge che, equivalentemente, è possibile tracciare un poligono, in questo caso un pentagono. Dunque in luogo a rette si utilizzano i (più comodi) segmenti che passano per ciascuna coppia di punti. in questo modo otteniamo un pentagono (cinque vertici e lati) regolare, e le proprie cinque diagonali. Dunque un totale di dieci rette passanti. Per non rovinare subito la sorpresa restiamo a tema e disegniamo altre due figure regolari, come abbiamo fatto per il pentagono. Il quadrilatero regolare, con quattro vertici e lati e le sue due diagonali: totale sei.
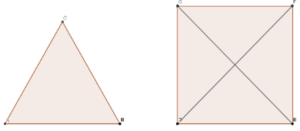
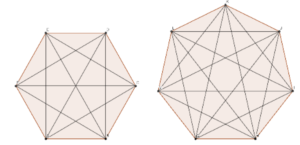
Ovviamente il triangolo equilatero non avendo diagonali, con i suoi tre lati e vertici, consta di sole tre rette passanti. Potremmo andare avanti a questo punto e prendere in esame l’esagono regolare, l’eptagono, ecc., ecc…. per controllare lati e diagonali, all’infinito. Invece mettiamo in tabella alcuni risultati ottenuti, vedendo se da essi possiamo ricavarne degli altri e fare delle congetture al riguardo.
| Punti | Rette |
| 3 | 3 |
| 4 | 6 |
| 5 | 10 |
Passando da tre a quattro punti notiamo che si aggiungono tre rette: è chiaro che ciascun punto deva “agganciarsi” a tutti gli altri rimanenti. Nel triangolo il punto A deve “agganciarsi” ai punti B e C, il punto B solamente al punto C; ciò perché BA e AB sono la stessa cosa: qui l’ordine non ha importanza! Abbiamo pertanto 2 + 1 = 3 collegamenti. Allo stesso modo nel quadrato abbiamo DE, DF, DG; EF, EG e FG. Partendo con D, esso si connette per tre volte a punti distinti, il punto E per due volte mentre al punto F resta un solo collegamento, in numeri: 3 + 2 + 1 = 6. Ancora, per cinque punti: 4 + 3 + 2 + 1 = 10. Da queste semplici constatazioni desumiamo che il legame che richiede l’esercizio di esprimere ha sicuramente a che fare con qualche progressione aritmetica. C’era d’aspettarselo: aggiungiamo un punto, e poi un altro e poi un altro… siamo noi stessi causando la progressione! Di conseguenza dovrebbe esserci un legame fra ciascuna coppia (Numero di punti, Numero di rette) e quella successiva (precedente) a seconda di come le vediamo.
Facciamo un’utile digressione: la più semplice delle progressioni aritmetiche è la somma fra i primi n numeri naturali. Senza dimostrarlo, come notò Johann Friedrich Carl Gauss, sappiamo che:
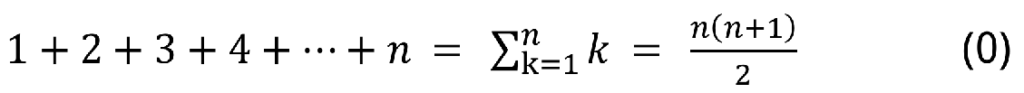
Raccogliamo ora altri dati sempre in tabella.
| Coppia | Punti | Rette |
| 1 | 3 | 3 |
| 2 | 4 | 6 |
| 3 | 5 | 10 |
| 4 | 6 | 15 |
| 5 | 7 | 21 |
Appare abbastanza chiaro che non potremo andare avanti a lungo nel tracciare e contare rette… altrimenti il quesito ci annienterà: man mano che i punti aumentano diventa sempre più difficile individuare e contare rette: provate con 10 punti! E che ne pensate di 100? Occorre una formula.
Ma prima osserviamo la tabella con le dovute attenzioni. Si nota che la somma di ciascuna coppia (punti, rette) è uguale al numero di rette della coppia successiva: per esempio la prima coppia in tabella (3,3) dà quale somma 6, come il numero di rette passanti per 4 punti. Allo steso modo la coppia due (4,6) che dà 10, è il numero di rette che passano per 5 punti… e così via. Se è così, allora il numero di rette passanti per n punti è dato dalla somma numerica della coppia precedente alla coppia che contiene n. Ovverosia, in formula:
Rn = (n − 1) + Rn−1 (1)
Provando ad applicare la (1) ad otto punti a tre a tre non allineati:
R8 = (8 − 1) + R8−1
che risulta:
R8 = (8 − 1 + R7) = 7 + R7 = 7 + (7 − 1 + R6) = 7 + 6 + (6 − 1 + R5) = = 7 + 6 + 5 + (5 − 1 + R4) = 7 + 6 + 5 + 4 + (4 − 1 + R3) = 7 + 6 + 5 + 4 + 3 + R3
Sappiamo che R3 = 3 = 2 + 1, quindi otteniamo esattamente quanto ci aspettavamo:
R8 = 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28
Dà 28 come la somma numerica della quinta coppia della tabella precedente (7,21): questo risultato ci permette di acquisire maggiore sicurezza rispetto alla congettura fatta osservando i numeri in tabella. Ciò è un risultato ma non una prova, non una dimostrazione. Possiamo dimostrare che tale formula sia vera (o smentirla) tramite il principio di induzione su N.
Si suppone che la proprietà P(n) sia vera per n, quindi supposta vera la (1), Rn = (n − 1) + Rn−1, (base dell’induzione), occorre verificare se valga anche P(n+1), ossia Rn+1 (passo induttivo), procediamo. Se è vero, allora sarà ∀n ∈ N[Pn].
Prima di procedere chiediamoci cosa ci aspettiamo. Abbiamo notato in precedenza che se passiamo, per esempio, da quattro a cinque punti, il numero di rette passanti aumenta di 4, ovvero quando da k = 4 si passa a k + 1 = 5 sappiamo che è sufficiente aggiungere k = 4 nuove rette a quelle precedenti, infatti se R4 = 6 ed R5 = 10 la differenza R5 – R4 = 4 ovvero k. Allo stesso modo dovremo verificare se passando da n ad n+1 punti il numero di rette verrà incrementato esattamente di n, la differenza Rn+1 – Rn.
Base dell’induzione
Abbiamo già verificato che per n = 8 vale R8 = (8 − 1) + R8−1 dunque supponiamo vera la
Rn = (n − 1) + Rn−1
Che risulta essere:
Rn = (n − 1) + (n − 2) + (n − 3) + ⋯ + 3 + 2 + 1
Passo induttivo
Per n + 1, a questo punto:
Rn+1 = n + (n − 1 + Rn−1 ) … = ⋯ n + (n − 1) + (n − 2) + (n − 3) + (n − 4) … + ⋯ (n − n + 3) + R3
Dove sappiamo
R3 = 3 = 2 + 1
Dunque risulta:
Rn+1 = n + (n − 1) + (n − 2) + (n − 3) + ⋯ + 3 + 2 + 1 = n + Rn
Come si vede il numero di rette è aumentato di n, infatti Rn+1 = n + Rn Q.E.D.
A questo punto potremmo concludere qui, salvo il fatto che la (1) ci dice solamente tutti i termini da sommare fra loro. Se i punti sono 1000 dovremo sommare tutti i termini compresi fra 999 e 1 ovvero, visti in ordine crescente, faremo 1 + 2 + 3 + 4 + 5 + ⋯ + 997 + 998 + 999 ma comunque ci toccherà eseguire una lunga somma: scomodo! Si tratta in ogni caso di una progressione aritmetica come la (0). Prima di arrivare a conclusione, notiamo ancora per mezzo di una tabella alcune altre importanti cose:
| Punti | Rette | Somma della coppia (punti, rette) |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 1 | 3 |
| 3 | 3 | 6 |
| 4 | 6 | 10 |
| 5 | 10 | 15 |
| 6 | 15 | 21 |
| 7 | 21 | 28 |
| 8 | 28 | 36 |
| 9 | 36 | 45 |
| 10 | 45 | 55 |
| 11 | 55 | 66 |
| 12 | 66 | 78 |
| 13 | 78 | 91 |
| 14 | 91 | 105 |
| 15 | 105 | 120 |
| 16 | 120 | 136 |
Sappiamo dalla (0) che la somma dei primi n numeri naturali è data da:
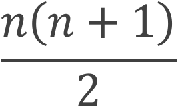
Che non fa esattamente al caso nostro in quanto, come si nota dalla tabella, il numero di rette è “spostato” verso il basso di una posizione rispetto alla somma della coppia (punti, rette). La somma della coppia (punti, rette) rappresenta, infatti, la somma dei primi n numeri naturali dove il numero di punti rappresenta n. Dire che è “spostato verso il basso di una posizione” significa per “perde” 1 rispetto alla somma dei primi n numeri.
Per “adattare” la (0) al nostro caso è sufficiente sottrarre 1 a tutti i termini da sommare:
(1 − 1) + (2 − 1) + (3 − 1) + (4 − 1) + ⋯ + (n − 1)
Ovvero, molto semplicemente:
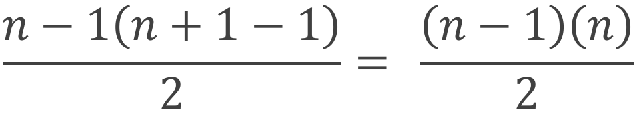
Allora il numero Rn delle rette passanti per n punti è dato da:
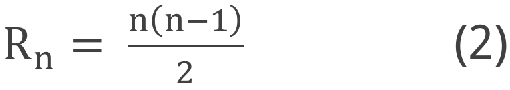
Ciò significa dire: il numero di rette Rn passanti per n punti dati è uguale alla metà del numero dei punti moltiplicato per la differenza fra il numero dei punti e l’unità.
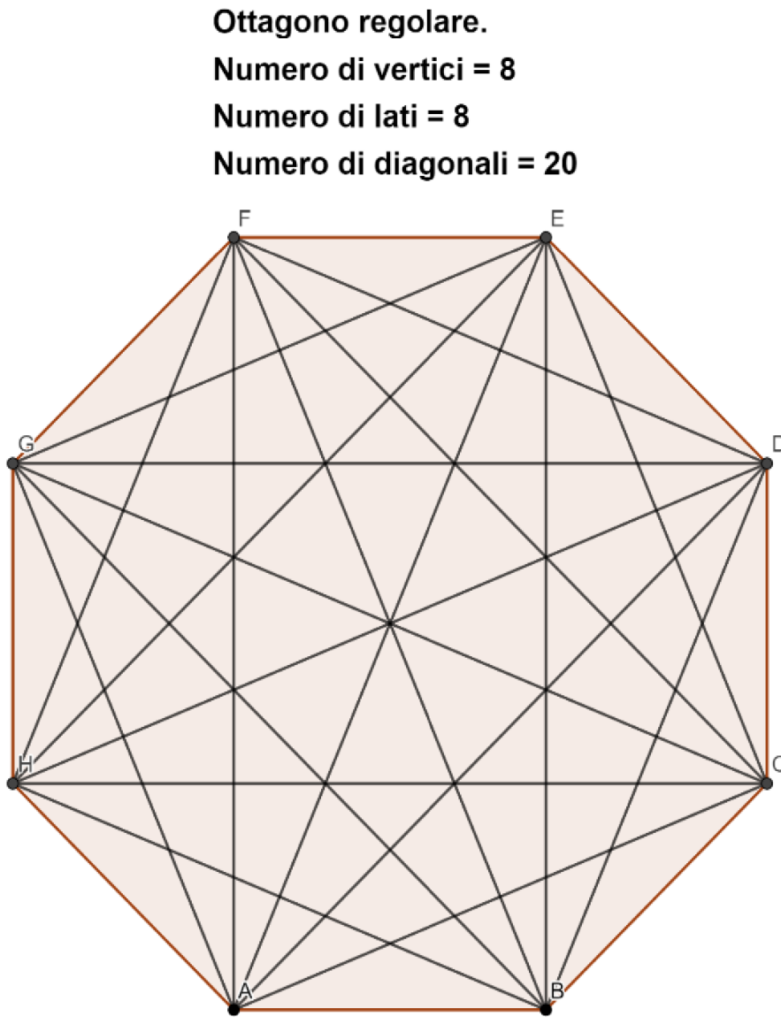
Abbiamo visto che determinare il numero di rette passanti per n punti a tre a tre non allineati equivale a fare la somma dei lati e delle diagonali di un poligono avente n vertici. Interessante è ora notare che se dal totale sottraiamo il numero dei lati ciò che si ottiene è il numero di diagonali. Così se il rettangolo ha quattro lati, ha anche due diagonali. La somma dei lati e delle diagonali è sei, come le rette passanti dell’esercizio appena risolto.
Siano d ed n, rispettivamente, il numero di diagonali e di lati di un poligono. Sottraendo n dalla (2) abbiamo che:
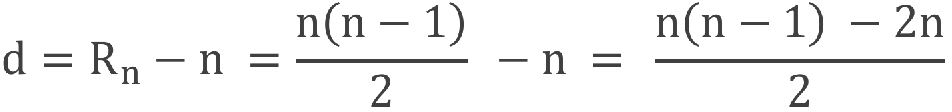
Dalla quale otteniamo
